Summer Camp
Welcome to this summer camp where you might be connected to the person next to you!
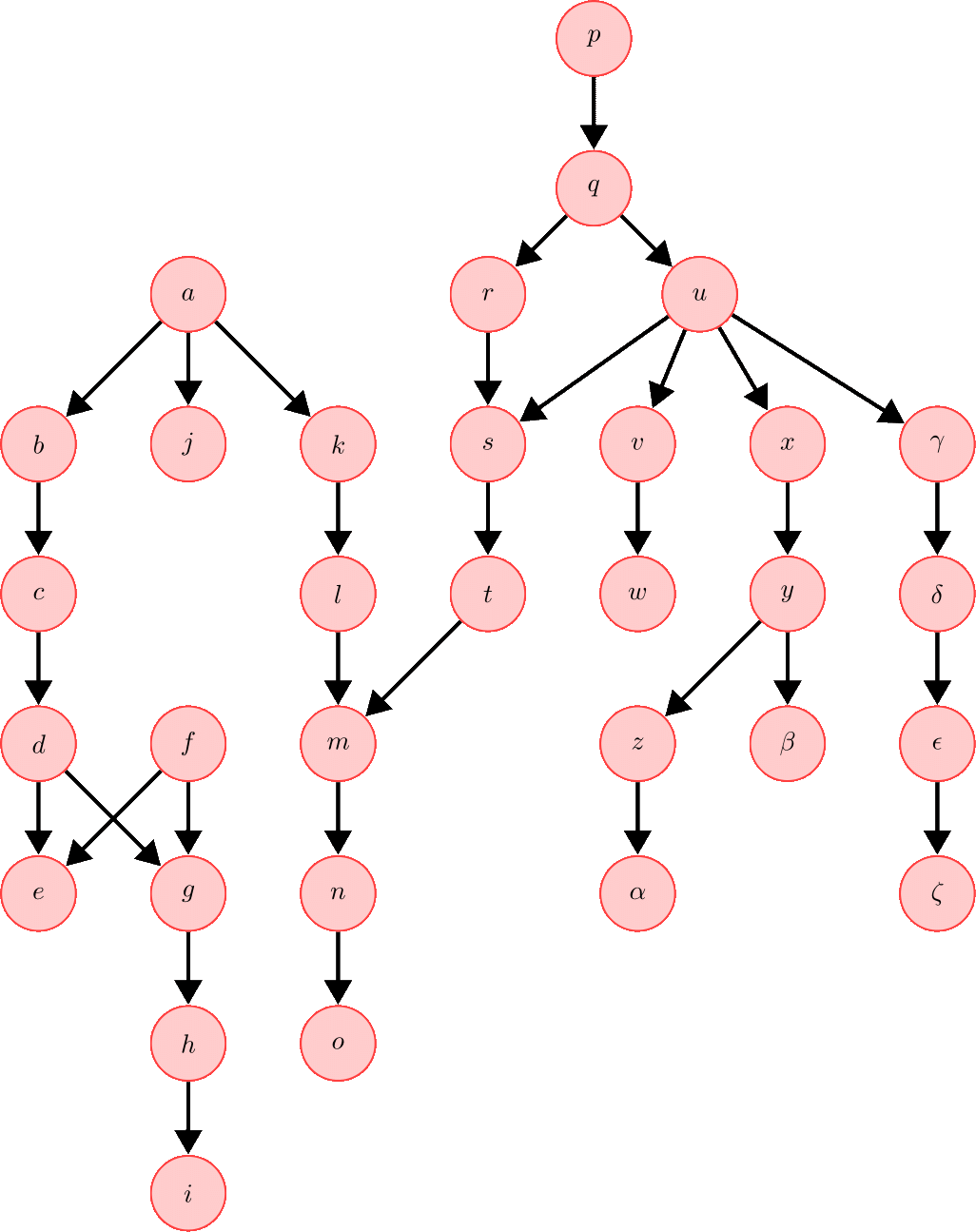
Participants
- I'm associated with the eighth problem in a list which is associated with another participant. (4)
- Did you know that \(3^2-2^3=1\)3²-2³=1 is the unique answer? (6)
- I often find that putting my belongings into drawers and shelves help me solve problems. (9)
- I arrived at the hotel in a coach last night. There were so many guests! (1)
- I came across a truly remarkable theorem today. (1)
- Could you fill up this bottle for me please? (3)
- I can help if you think the binomial distribution has too many limitations. (7)
- I think cylinders function well. (2)
- I carry these chains around all the time. (2)
- What a beautiful equation - who would've thought these constants are all related to each other! (3)
- I introduced the first problem in a list which is associated with another participant. (5)
- I generalized the integral first rigorously defined by another participant and now I have my own! (6)
- My inequality follows directly from an inequality associated with another participant. (5)
- This is the least well-behaved function I've ever seen - its derivative doesn't exist! (3)
- If a little theorem doesn't satisfy you, don't worry, I've got a great theorem! (6)
- I love collaborating with others. (5)
$$\small \begin{align}
& \beta + \delta - z + \left\lfloor \frac{l}{30} \right\rfloor + \frac{1}{2}(v-s-r)(\zeta-g-\left\lfloor \frac{\epsilon}{42} \right\rfloor -2) + ceijk(w+\left\lfloor \frac{t-u}{4} \right\rfloor)\\
& - \left\lfloor adx(b+oy) \left(3fy \left( \beta - \left\lfloor \frac{q}{17} \right\rfloor + 15 \right) + \left(p - \left\lfloor \frac{z}{10} \right\rfloor + 7 \right) \left(h + \left\lfloor \frac{l}{62} \right\rfloor +1 \right) - \gamma - \frac{n}{2} -2 \right) \times 10^{-\left\lfloor \frac{\alpha}{m} \right\rfloor-2} \right\rfloor
\end{align}$$
β+δ-z+floor(l/30)+1/2×(v-s-r)(ζ-g-floor(ε/42)-2)+ceijk(w+floor((t-u)/4))-floor(adx(b+oy)(3fy(β-floor(q/17)+15)+(p-floor(z/10)+7)(h+floor(l/62)+1)-γ-n/2-2)×10^(-floor(α/m)-2))
Hint: \(\Sigma = 1034339\)Σ = 1034339
The following calculator is only provided for convenience and is otherwise not part of the puzzle.
| \(a\) | \(b\) | \(c\) | \(d\) | \(e\) | \(f\) | ||||||
| \(g\) | \(h\) | \(i\) | \(j\) | \(k\) | \(l\) | ||||||
| \(m\) | \(n\) | \(o\) | \(p\) | \(q\) | \(r\) | ||||||
| \(s\) | \(t\) | \(u\) | \(v\) | \(w\) | \(x\) | ||||||
| \(y\) | \(z\) | \(\alpha\) | \(\beta\) | \(\gamma\) | \(\delta\) | ||||||
| \(\epsilon\) | \(\zeta\) |
Result: